Prefix-sum can solve many sub-array sum problems. We can maintain the sum of array[0:i] to solve this kind of problems.
What is Prefix-Sum?
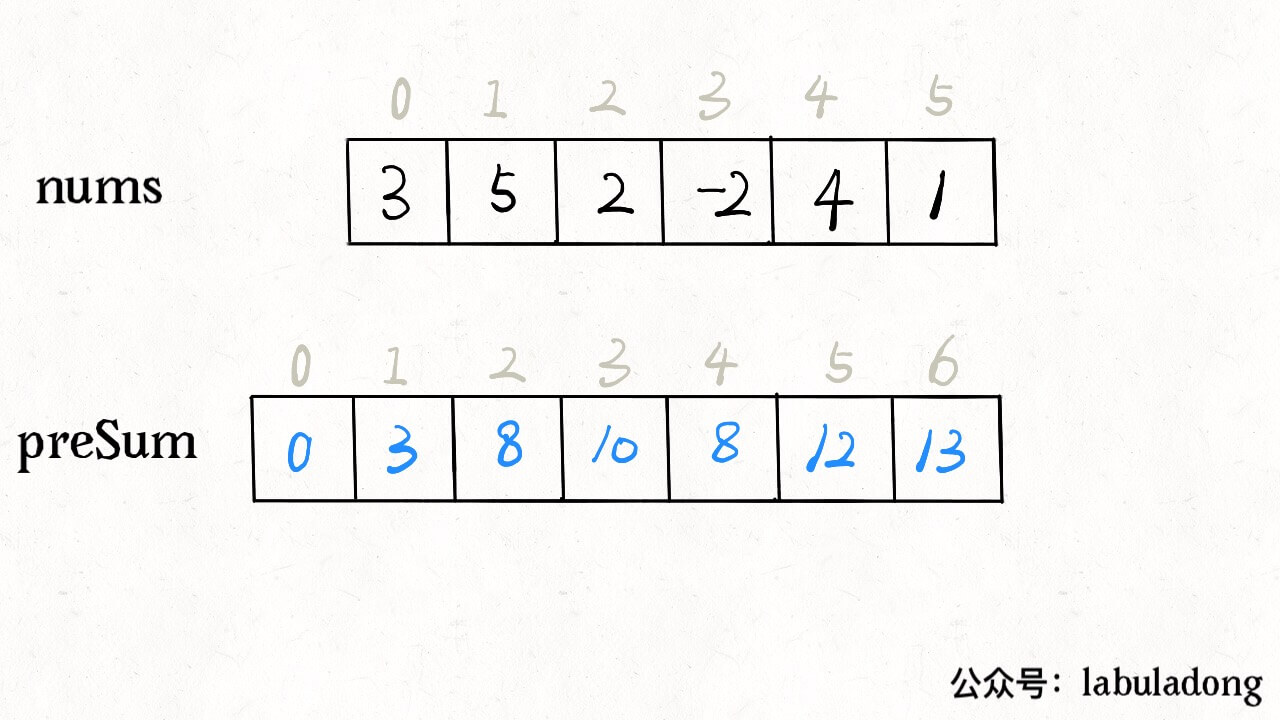
preSum[i] is the sum of nums[0:i-1]. If we want the sum of nums[i:j+1], we can use presum[j+1]-prefix[i]
Sample Problems in Leetcode
560. Subarray Sum Equals K
Given an array of integers nums and an integer k, return the total number of continuous subarrays whose sum equals to k.
Example 1:
Input: nums = [1,1,1], k = 2
Output: 2
Example 2:
Input: nums = [1,2,3], k = 3
Output: 2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution:
def subarraySum(self, nums: List[int], k: int) -> int:
dict_t = {}
curr_sum = 0
res = 0
for i in range(len(nums)):
curr_sum += nums[i]
## from 0 to i
if curr_sum == k:
res += 1
## from where sum = curr_sum - k to i
if curr_sum - k in dict_t.keys():
res += dict_t.get(curr_sum - k)
## one more i having curr_sum
if curr_sum not in dict_t.keys():
dict_t[curr_sum] = 1
else:
dict_t[curr_sum] += 1
return res
523. Continuous Subarray Sum
Given an integer array nums and an integer k, return true if nums has a continuous subarray of size at least two whose elements sum up to a multiple of k, or false otherwise.
An integer x is a multiple of k if there exists an integer n such that x = n * k. 0 is always a multiple of k.
Example 1:
Input: nums = [23,2,4,6,7], k = 6
Output: true
Explanation: [2, 4] is a continuous subarray of size 2 whose elements sum up to 6.
Example 2:
Input: nums = [23,2,6,4,7], k = 13
Output: false
Here we see the “subarray sum” again, so we consider use prefix-sum.
How can the (sum_subarray1 - sum_subarray2) % k == 0? Iff there remainings while divide by k are the same!
Another corner case we need to consider is the for 0s, they can be divided by any k.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution:
def checkSubarraySum(self, nums: List[int], k: int) -> bool:
dict_t = {}
curr_sum = 0
for i in range(len(nums)):
curr_sum += nums[i]
remaining = curr_sum % k
if i >= 1 and remaining == 0:
return True
if remaining in dict_t.keys() and i - dict_t.get(remaining) > 1:
return True
# here we only store the index which is the smallest among those who have the same remaining
if remaining not in dict_t.keys():
dict_t[remaining] = i
return False
238. Product of Array Except Self
Given an integer array nums, return an array answer such that answer[i] is equal to the product of all the elements of nums except nums[i]
You must write an algorithm that runs in O(n) time and without using the division operation.
This is a problem of subarray product, however it’s similar to the sum problem.
$res[i] = product[0:i] * product[i+1:len(nums)]$
Other Prefix-Sum Problems
- https://leetcode.com/problems/maximum-sum-of-3-non-overlapping-subarrays/
- https://leetcode.com/problems/maximum-size-subarray-sum-equals-k/
- https://leetcode.com/problems/number-of-submatrices-that-sum-to-target/
- https://leetcode.com/problems/max-sum-of-rectangle-no-larger-than-k/
- https://leetcode.com/problems/binary-subarrays-with-sum/
- https://leetcode.com/problems/path-sum-iii/
- https://leetcode.com/problems/subarray-sums-divisible-by-k/
- https://leetcode.com/problems/range-sum-query-2d-immutable/
- https://leetcode.com/problems/count-number-of-nice-subarrays/
- https://leetcode.com/problems/matrix-block-sum/
References
https://leetcode.com/discuss/general-discussion/563022/prefix-sum-problems