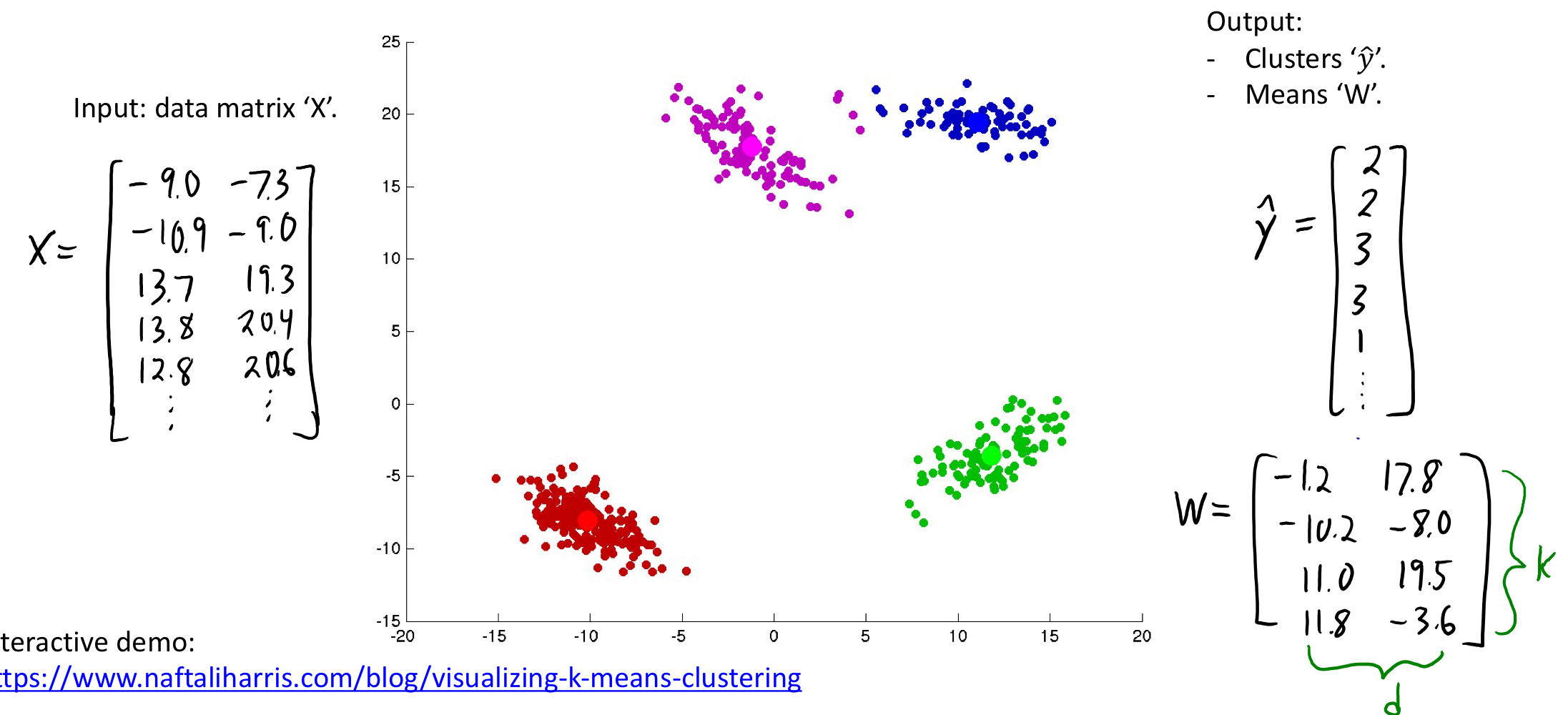
clustering
- input: a set of examples described by features $x_i$
- output: an assignment of examples to groups
K-Means
The most popular clustering method
Input:
- the number of clusters hyper-parameter k
- intial guess of the mean for each cluster
Algorithm:
- Assign $x_i$ to its closest mean
- Update the means
- Repeat until converges
K-Means Issues
- how to determine K
- each example is assigned to one and only one cluster
- may converge to a sub-optimal solution
- only solve convex problems
KNN vs. K-Means
| Property | KNN | K-Means |
|---|---|---|
| Task | Supervised Learning | Unsupervised Learning |
| Meaning of “K” | Number of neighbours | Numer of clusters |
| Intialization | No training phase | Training is sensative to initilialzation |
| Model Complexity | More complicated for small K | Simpler for small K |
| Parametric? | Non-Parametric | Parametric - K depends on n |
Cost of K-Means
We need to calculate $n$ examples to $k$ clusters, each time costs $d$ time. So the total complexity for calculating distance is $O(ndk)$
Use of K-Means - Vector Quantization
Give a set of data, run K-Means, use the means to replace the data belongs to the specific cluster.
Density-Based Clustering (DBSCAN)
- clusters are defined by “dense” regions, non-dense regions are not clustered
- can be non-convex
- non-parametric (no fixed number of clusters k)
DBSCAN Algorithm
Two hyperparams:
- Epsilon($\epsilon$): distance we use to decide if another point is “neighbour”
- MinNeighours: number of neighbours needed to say a region is dense
For each example $x_i$:
- If $x_i$ is already in a cluster, do nothing
- Else test whether $x_i$ is a core point ( >= minNeighbour neighours within $\epsilon$)
- if not, do nothing
- else, make a new cluster and call expand cluster function
Expand Cluster Function
- assign all neighbours to $x_i$ cluster
- for each new “core” point, call “expand cluster” recursively
Issues
- some points are not assigned
- sensitvie to the choice of $\epsilon$ and minNeighbours (but not sensivtive to initialization)
- finding cluster for a new point is expensive (need to compute distances to all core points)
- in high dimensions, need a lot of points to fill the space
Hierarchical Clustering
Sometimes we have different densities:
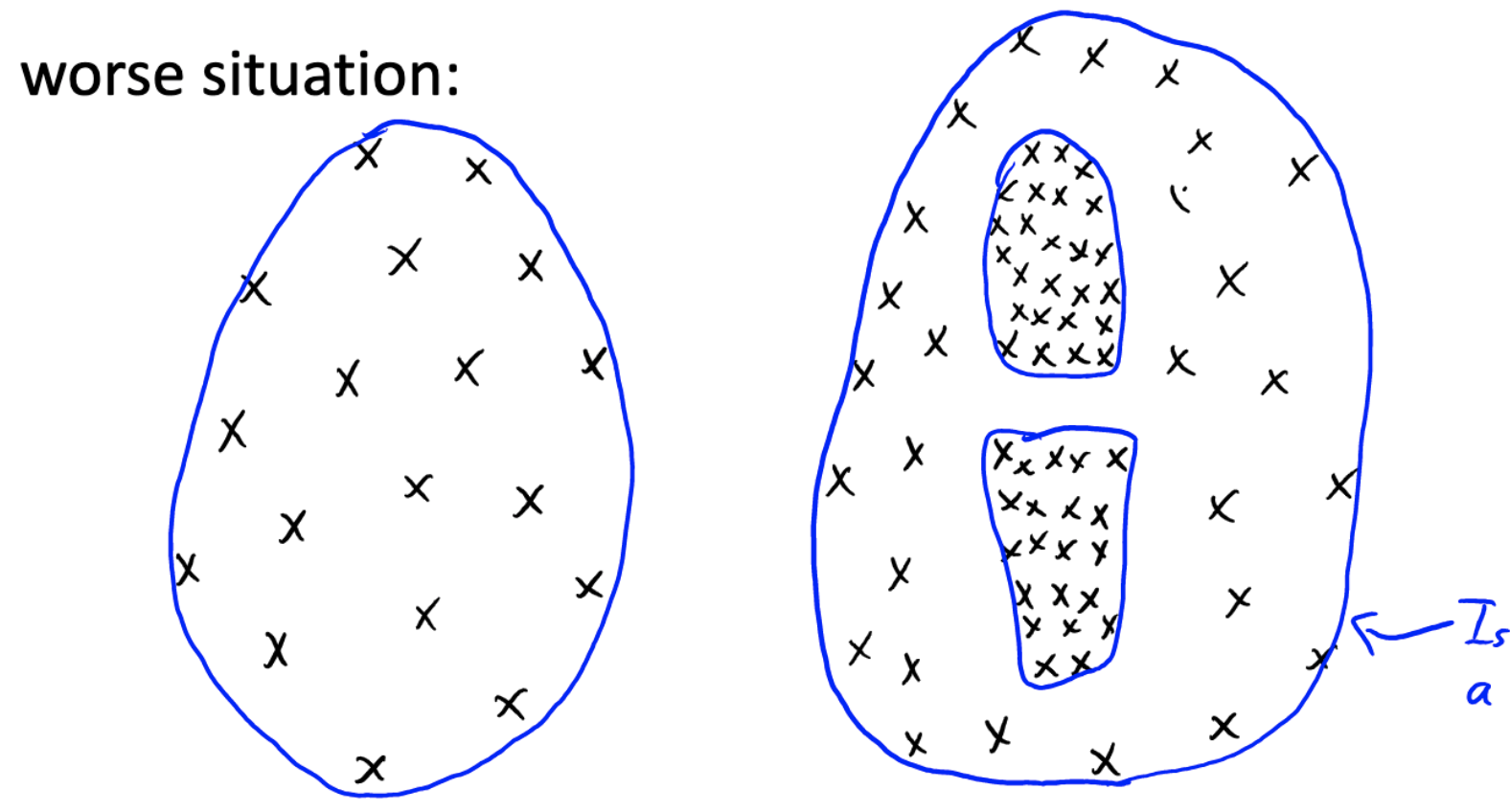
we can use hierarchial clustering to produce a tree of clusterings.
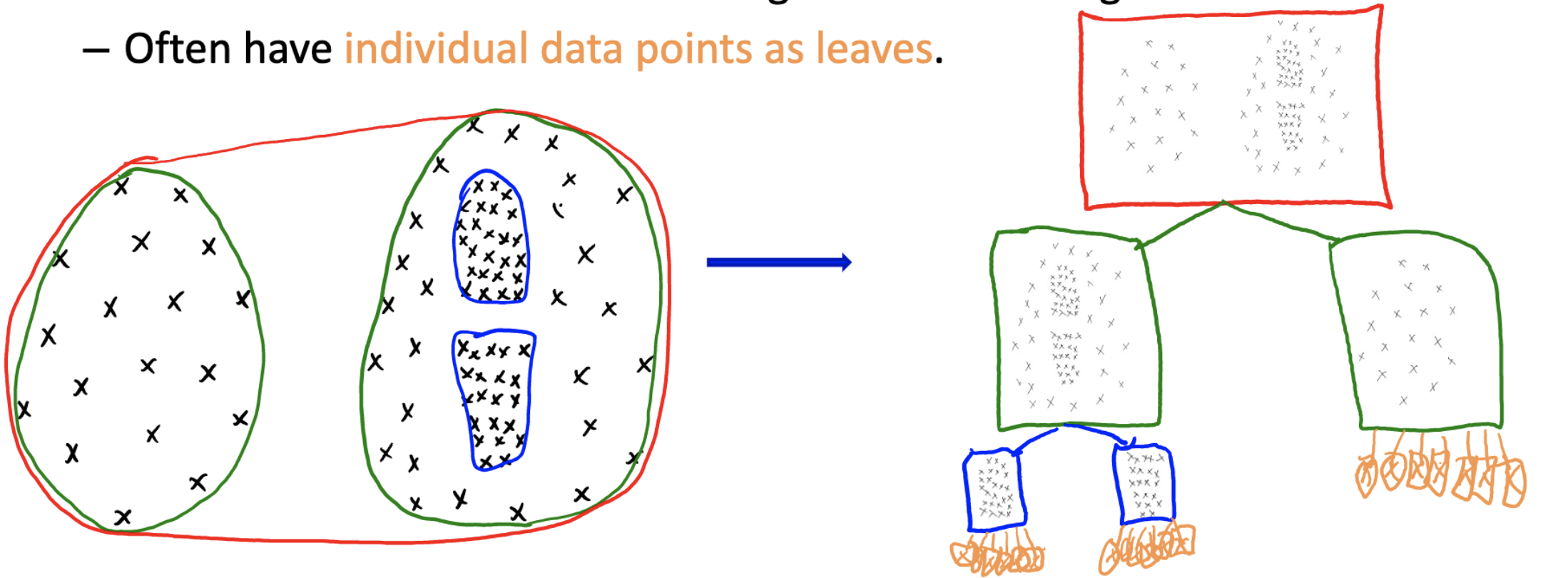
Agglomerative(Bottom-Up) Clustering
- Starts with each point in its own cluster
- Each step merges the two “closest” clusters
- Stop with one big cluster that has all points
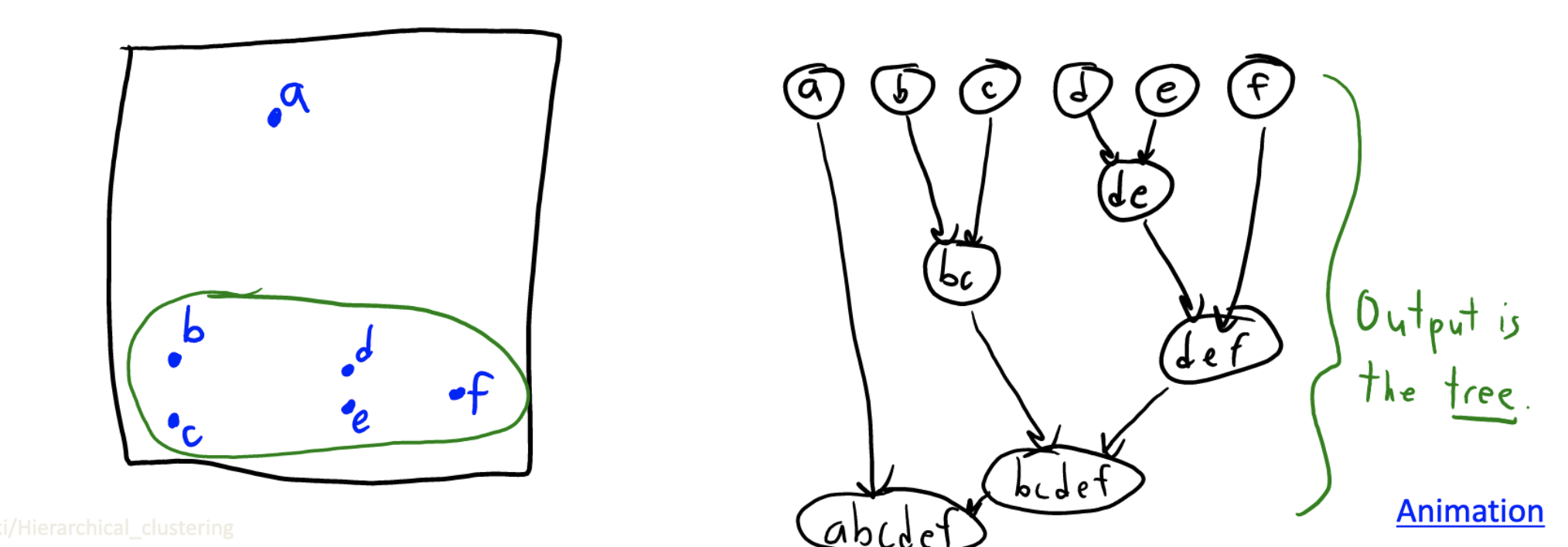
Cost: $O(n^3d)$ - each step costs $n^2d$, might only merge 1 new point every step