Cycles
We can use Floyd algorithm to solve problems like this.
141. Linked List Cycle
Given head, the head of a linked list, determine if the linked list has a cycle in it.
Return true if there is a cycle in the linked list. Otherwise, return false.
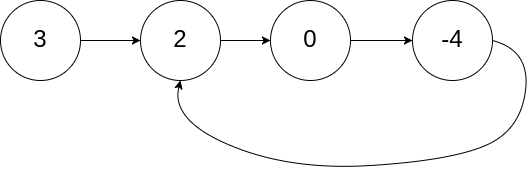
If there is a cycle in the linkedlist, the fast point will finally catch the slow point.
1
2
3
4
5
6
7
8
9
10
11
class Solution:
def hasCycle(self, head: Optional[ListNode]) -> bool:
fast, slow = head, head
while fast and fast.next:
fast = fast.next.next
slow = slow.next
if fast == slow:
return True
return False
142. Linked List Cycle II
How about find the cycle start?
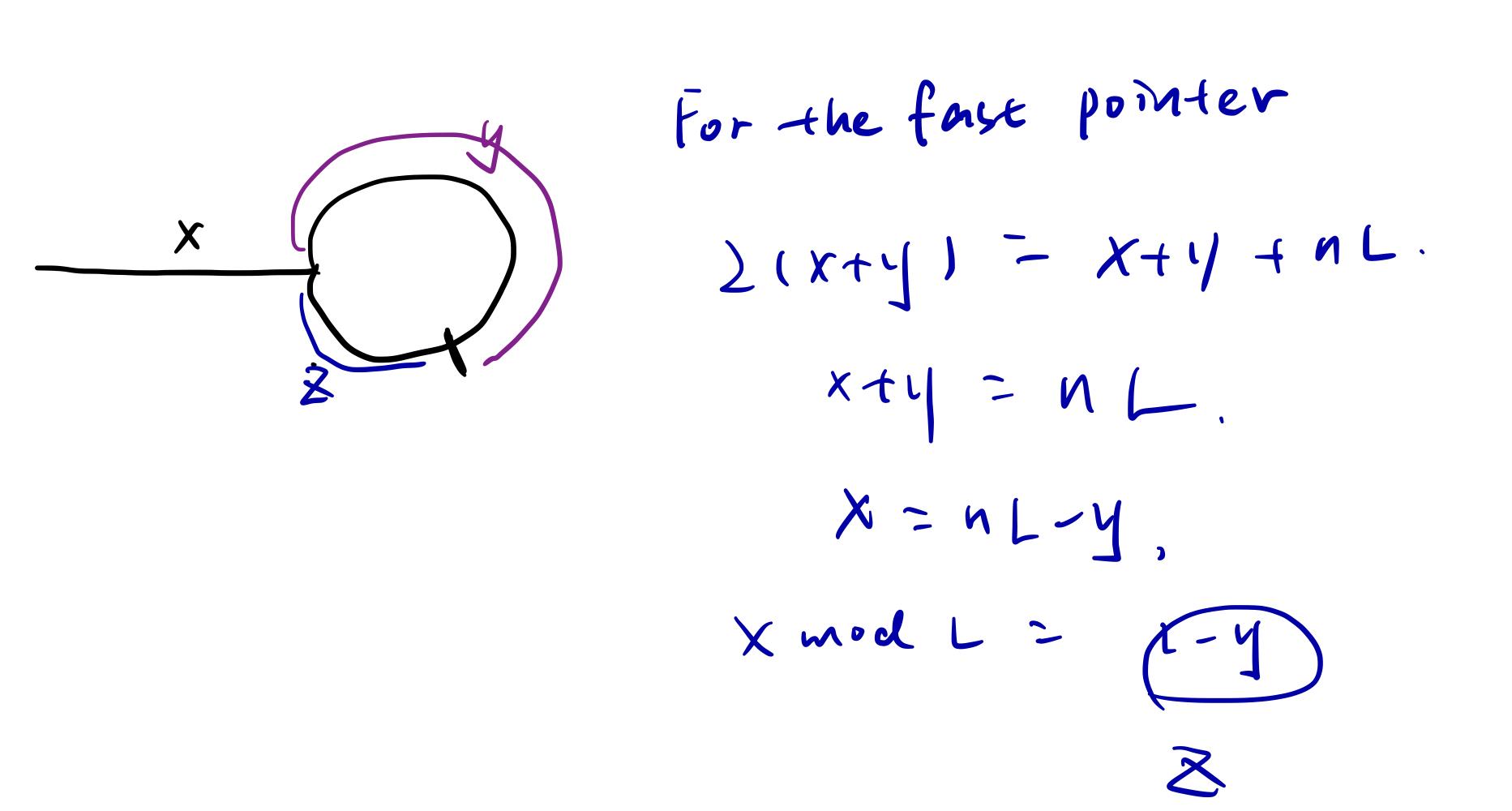
After we find out the meeting point, we start from head and the meeting point - then they will meet at the start of the point.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
def detectCycle(self, head: Optional[ListNode]) -> Optional[ListNode]:
fast, slow = head, head
while fast and fast.next:
fast = fast.next.next
slow = slow.next
if fast == slow:
slow = head
while slow != fast:
slow = slow.next
fast = fast.next
return slow
202. Happy Number
A happy number is a number defined by the following process:
- Starting with any positive integer, replace the number by the sum of the squares of its digits.
- Repeat the process until the number equals 1 (where it will stay), or it loops endlessly in a cycle which does not include 1.
- Those numbers for which this process ends in 1 are happy.
- Return true if n is a happy number, and false if not.
Input: n = 19
Output: true
Explanation:
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
Any number n should belongs to below scenarios:
- end up with 1
- run into a cycle but will finally hit the same number it got before
- continuesly going higher and higher
we don’t need to worry about the 3rd scenario - even the largest n’s digits square sum is not large.
For the scenario 1 and 2, we can consider this problem as whether there is a cycle in the list - slow pointer get_next once each time, fast pointer get_next twice each time.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution:
def isHappy(self, n: int) -> bool:
def get_next(n):
total_sum = 0
while n > 0:
n, digit = n // 10, n % 10
total_sum += digit ** 2
return total_sum
slow = n
fast = get_next(n)
while fast != 1 and slow != fast:
slow = get_next(slow)
fast = get_next(get_next(fast))
return fast == 1
287. Find the Duplicate Number
Given an array of integers nums containing n + 1 integers where each integer is in the range [1, n] inclusive.
There is only one repeated number in nums, return this repeated number.
You must solve the problem without modifying the array nums and uses only constant extra space.
The hard part is that we cannot modify the array and use extra space.
Since there is only one repeated number, we can consider the Floyd’s Cycle Detection algorithm.
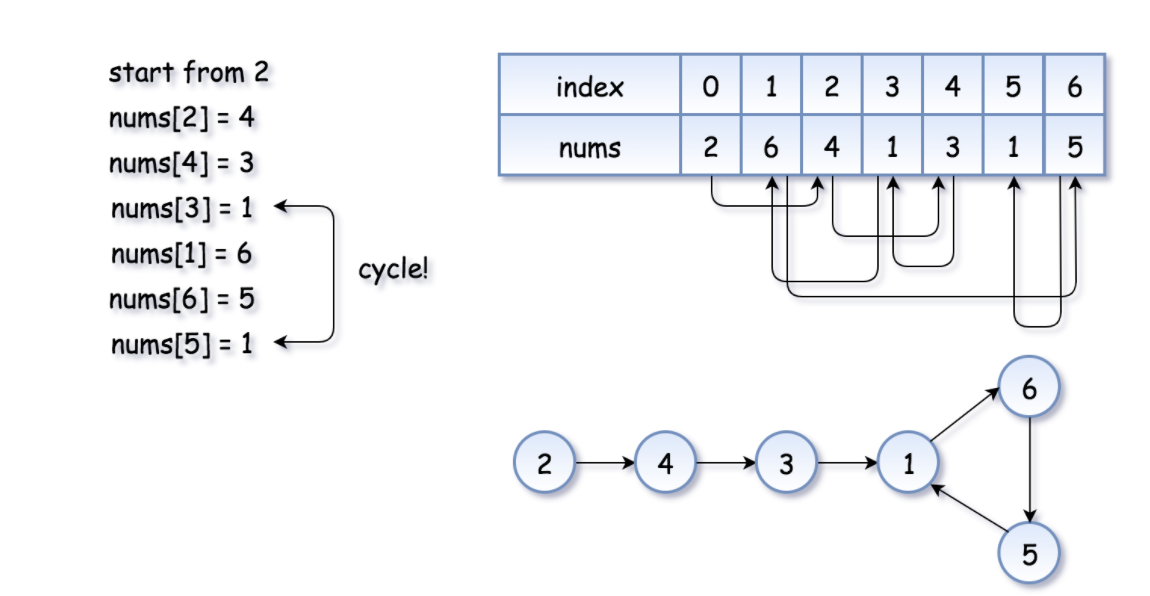
If there are two pointer points to the same number, then the number is the duplicate number.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution:
def findDuplicate(self, nums: List[int]) -> int:
fast = slow = nums[0]
while True:
fast = nums[nums[fast]]
slow = nums[slow]
if fast == slow:
break
# start from head to find the head of cycle
slow = nums[0]
while slow != fast:
slow = nums[slow]
fast = nums[fast]
return slow
457. Circular Array Loop
array nums[i]/ If nums[i] is positive, move nums[i] steps forward, and if nums[i] is negative, move nums[i] steps backward. A cycle in the array consists of a sequence of indices seq of length k where:
- Following the movement rules above results in the repeating index sequence seq[0] -> seq[1] -> … -> seq[k - 1] -> seq[0] -> …
- Every nums[seq[j]] is either all positive or all negative. (move in the same direction)
- k > 1
Return true if there is a cycle in nums, or false otherwise.
Since it’s talking about the circular in a array, we can consider use the fast and slow pointer, but the problem has a lot of resctrictions on the qualified sequence, some limitations should apply while finding.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution:
def circularArrayLoop(self, nums: List[int]) -> bool:
# find the next index to handle the index which is out of boudary
def get_next(index: int):
return (index + nums[index] + n) % n
n = len(nums)
for i in range(n):
slow = fast = i
# slow pointer's next direction, fast pointers inter direction, fast pointer next direction should be the same
while nums[slow] * nums[get_next(fast)] > 0 and nums[slow] * nums[get_next(get_next(fast))] > 0:
slow = get_next(slow)
fast = get_next(get_next(fast))
if slow == fast:
# the length of the circular array should be larger than 1
if slow == get_next(slow):
break
return True
# optimization step, the indices we have already passed through should be opt out.
j = i
val = nums[i]
while nums[j] * val > 0:
temp = get_next(j)
nums[j] = 0
j = temp
return False
Fast and Slow Pointers
143. Reorder List
$L0 → L1 → … → L_{n - 1} → Ln => L0 → Ln → L1 → L_{n - 1} → L2 → L_{n - 2} → …$
Three steps:
- Find middle node
- Reverse the second half
- Merge 1st and 2nd half
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution:
def reorderList(self, head: Optional[ListNode]) -> None:
"""
Do not return anything, modify head in-place instead.
"""
slow = fast = head
# find middle node
while fast and fast.next:
fast = fast.next.next
slow = slow.next
# reverse from slow
prev = None
while slow:
slow.next, prev, slow = prev, slow, slow.next
# merge (len(1st half) = len(2nd half) or len(2nd half) + 1)
curr1, curr2 = head, prev
# here we need to check curr2.next (we don't want to merge the last node of curr2 because it's included in the first half)
while curr2.next:
curr1.next, curr2.next, curr1, curr2 = curr2, curr1.next, curr1.next, curr2.next
19. Remove Nth Node From End of List
Given the head of a linked list, remove the nth node from the end of the list and return its head.
Input: head = [1,2,3,4,5], n = 2
Output: [1,2,3,5]
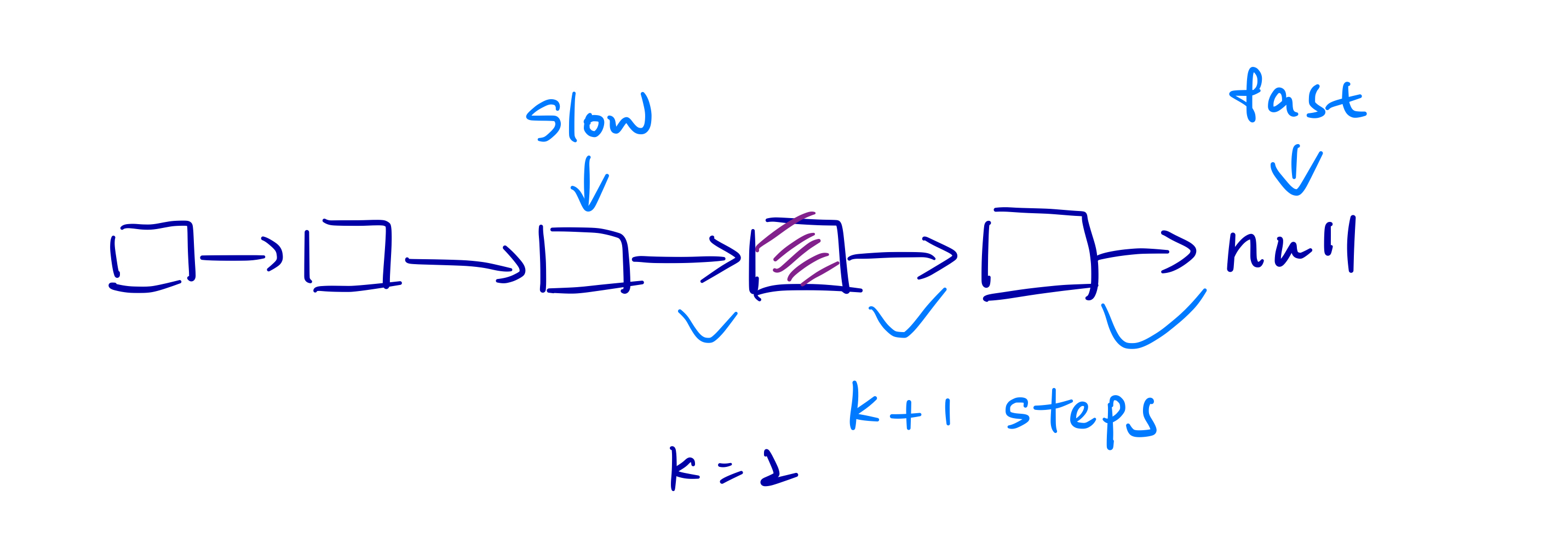To remove the nth node from the end, we should find out the n+1th node from the node. So the fast and slow pointer should have n+1 intervals.
1
2
for _ in range(n+1):
fast = fast.next
To handle the case that the list will be empty after removing, which means slow.next might be null for this case.
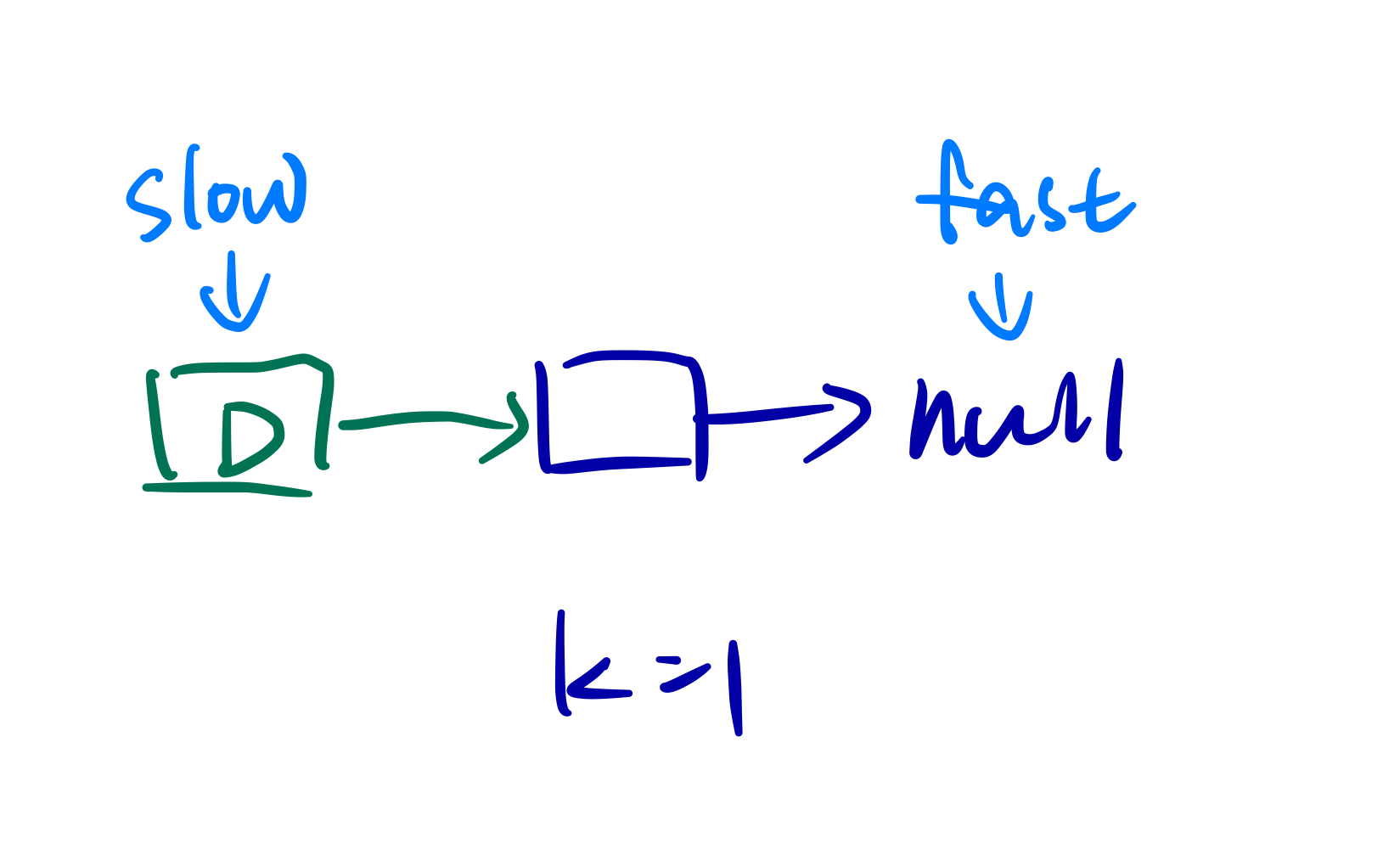we should add a dummy node, and return dummy.next
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def removeNthFromEnd(self, head: Optional[ListNode], n: int) -> Optional[ListNode]:
dummy = ListNode(0)
dummy.next = head
slow = fast = dummy
for _ in range(n+1):
fast = fast.next
while fast:
fast = fast.next
slow = slow.next
slow.next = slow.next.next
return dummy.next
