50. Pow(x, n)
Implement pow(x, n), which calculates x raised to the power n (i.e., $x^n$).
The simplest way is to multiply n times, time complexity is $O(n)$
Another way is to think $x^{10}$ as $x^5 * x ^5$ , then divide $x^5$ as $x^2 * x^3$ until $x^0$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution:
def myPow(self, x: float, n: int) -> float:
def helper(x: float, n: int):
if x == 0:
return 0
if n == 0:
return 1
half = helper(x, n //2)
if n % 2 == 0:
return half * half
else:
return half * half * x
res = helper(x, n)
return res if n >= 0 else 1/res
191. Number of 1 Bits
Write a function that takes an unsigned integer and returns the number of ‘1’ bits it has.
n & (n-1) will change the n’s last 1 to 0
1
2
3
4
5
6
7
class Solution:
def hammingWeight(self, n: int) -> int:
res = 0
while n != 0:
res += 1
n &= n-1
return res
Bit Manipulation
- 190. Reverse Bits
- [67. Add Binary]
190. Reverse Bits
Reverse bits of a given 32 bits unsigned integer.
For a base-10 case:
1
2
ans = ans * 10 + n % 10
n /= 10
For a base-2 case, it’s similar:
1
2
ans = ans * 2 + n % 2
n /= 2
However we cannot do this, because it will ignore the zeros which are in the front of the base-2 number, like 00000010100101000001111010011100. (In the base-10 case, it will not happen, since there would not be a number like 00089)
Also, for Java case, there is no unsigned int in java, so the number might be 1111111111…1, which is a negative number, we should use bit manipulation to handle the negative number.
- How to get the last number of n? => n & 1
-
How to get the ans? => ans « 1 n & 1 ( which is the same as ans * 2 + n % 2)
Then the answer would be:
1
2
3
4
5
6
7
8
class Solution:
def reverseBits(self, n: int) -> int:
res = 0
for i in range(32): # we are sure that we need to handle 32 bits
res = (n & 1) | res << 1
n >>= 1
return res
67. Add Binary
Given two binary strings a and b, return their sum as a binary string.
Input: a = “11”, b = “1”
Output: “100”
a ^ b => the sum without carry
a & b « 1 => carry
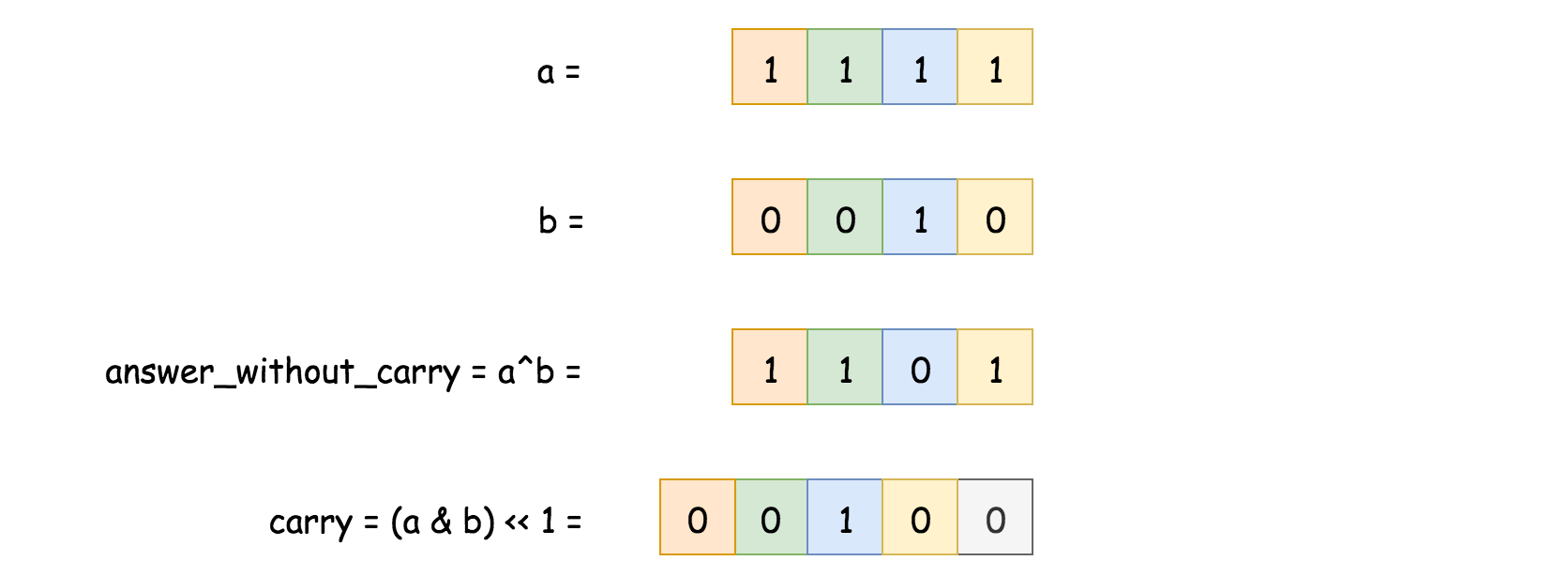
sum = the sum without carry + carry
1
2
3
4
5
6
7
class Solution:
def addBinary(self, a: str, b: str) -> str:
a = int(a, 2)
b = int(b, 2)
while b != 0:
a, b = a ^b, (a&b)<<1
return bin(a)[2:]