L2-Regularization
Standard regularization strategy is L2-regularization. Also called ridge regression
| $f(w) = \frac{1}{2} | Xw-y | ^2 + \frac{\lambda}{2} | w | ^2$ |
Intuition: Large slope w tends to lead to overfitting. Large $\lambda$ puts large penalty on overfitting.
L2-Regularization Normal Equations

L2-Regularization Gradient Descent
$f(w) = \frac{1}{2}||Xw-y||^2 + \frac{\lambda}{2}||w||^2$
$f’(w) = X^T (Xw-y) + \lambda w$
$w^{t+1} = w^t - \alpha f’(w)$
Standarizating Features
Features may have different scales.
- it doesn’t matter for decsion tree or naive bayes because they look only one feature at a time.
- doesn’t matter for least squares
- matter for KNN - distance will be controlled by large scale features
- matter for regularized least squares - Penalizing ($w_j^2$) means different things if features ‘j’ are on different scales.
Steps:
For each feature:
- compute mean and standard variation
- substract mean and divide by standard variation
Standarizating Targets
In regression, we sometimes need to standandize y.
Gaussian RBF: A sum of bumps
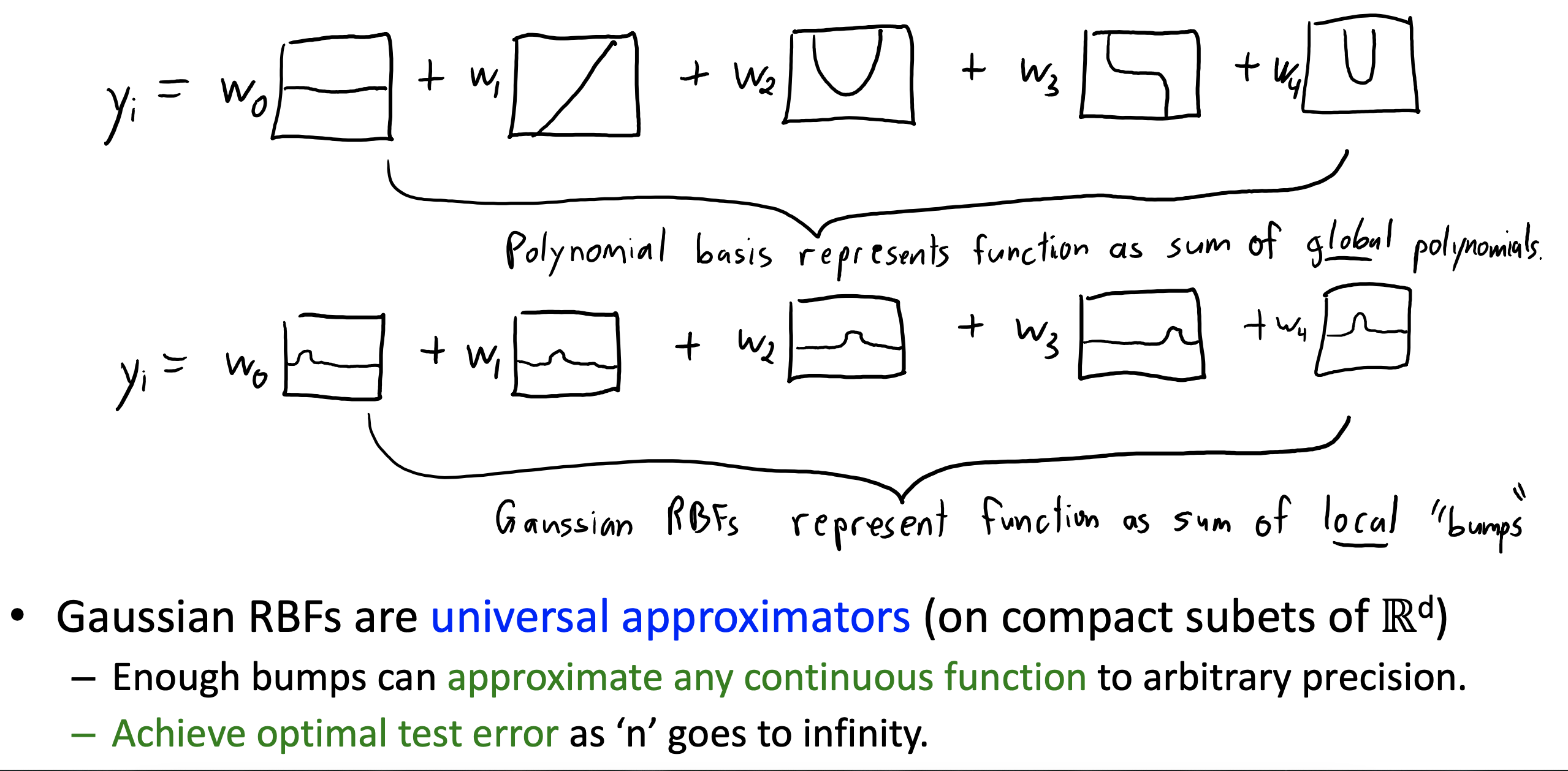
What is radial basis functions (RBFs)?
| A set of non-parametric bases that depend on distances to training points. Replace $x_i = (x_{i1}, x_{i2}, …, x_{id})$ with $z_i = (g( | x_i-x_1 | , g( | x_i-x_2 | ), …, g( | x_i-x_n | ))$ |
Gaussian RBF: $g(\epsilon) = exp(-\frac{\epsilon ^ 2}{2\theta ^ 2})$
How to avoid using huge number of features?
- we regularize $w$ and use validation error to choose $\sigma$ and $\lambda$
L1-Regularization (Lasso)
Simultaneously regularizes and select features
| $f(w) = \frac{1}{2} | Xw-y | ^2 + \lambda | w | _1$ |
Regularization and Sparsity
L2 doesn’t give sparsity but L1 gives.

L1 Loss Vs. L1 Regularization
L1 loss is robust to outlier datapoints. L1 regularization is robust to irrelevant features.
Combine L1 loss and L1 regularization $f(w) = ||Xw-y|| + \lambda||w||_1$
L* Regularization

