Find minimum in sorted array
153. Find Minimum in Rotated Sorted Array
Leetcode 153
Suppose an array of length n sorted in ascending order is rotated between 1 and n times.
For example, the array nums = [0,1,2,4,5,6,7] might become:
[4,5,6,7,0,1,2] if it was rotated 4 times.
[0,1,2,4,5,6,7] if it was rotated 7 times.
Notice that rotating an array [a[0], a[1], a[2], …, a[n-1]] 1 time results in the array [a[n-1], a[0], a[1], a[2], …, a[n-2]].
Given the sorted rotated array nums of unique elements, return the minimum element of this array. You must write an algorithm that runs in $O(log n)$ time.
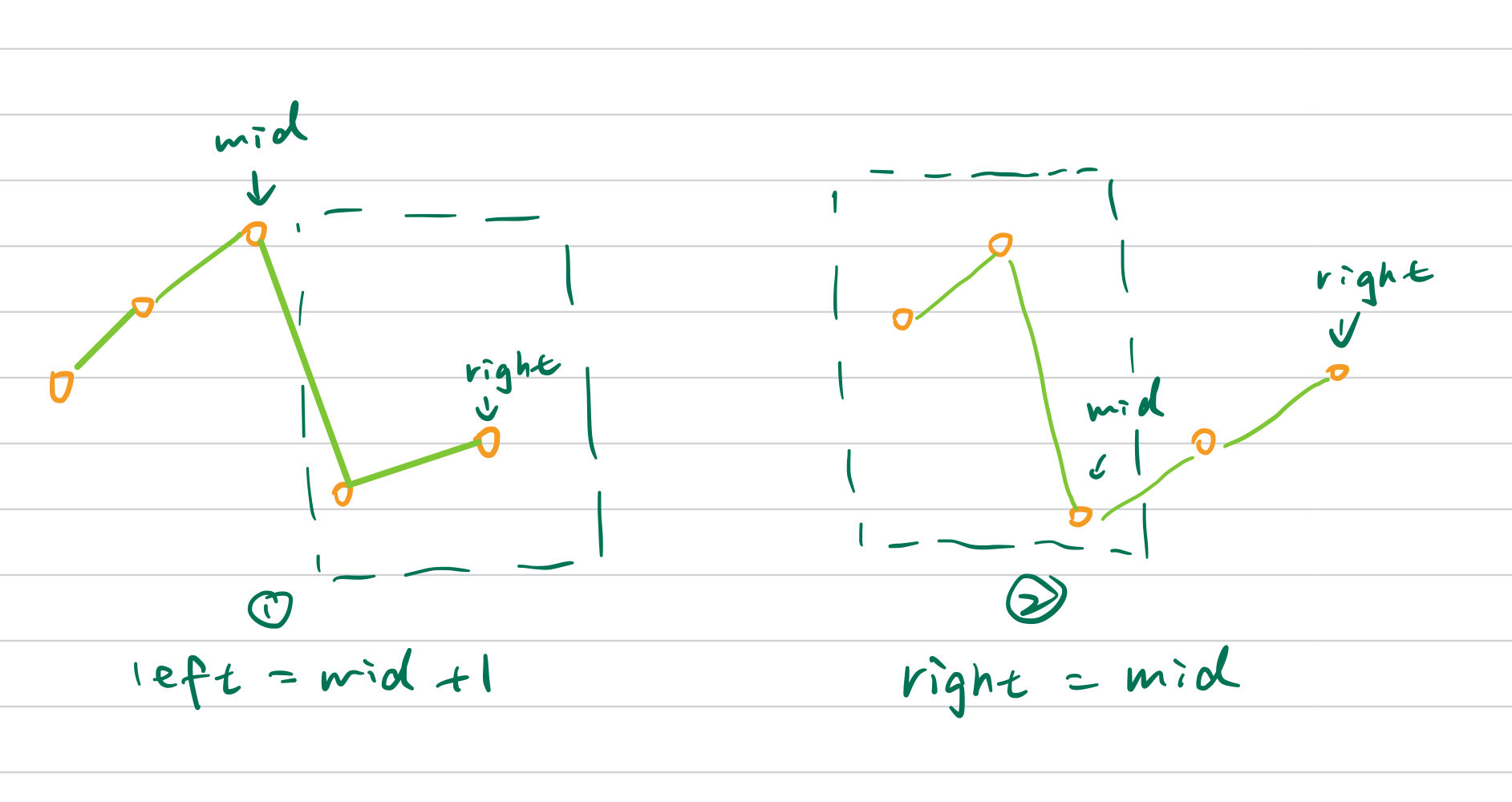
We have two scenarios:
- nums[mid] > nums[right], which means the right half is rotated, so we set left = mid + 1
- nums[mid] <= nums[right], which means the left half is rotated, so we set right = mid (here we set right = mid instead of mid -1, because the right itself might be the minimum element)
1
2
3
4
5
6
7
8
9
10
11
12
class Solution:
def findMin(self, nums: List[int]) -> int:
left, right = 0, len(nums) - 1
while left < right:
mid = left + (right - left) // 2
if nums[mid] <= nums[right]:
right = mid
else:
left = mid + 1
return nums[left]
154. Find Minimum in Rotated Sorted Array II
Suppose an array of length n sorted in ascending order is rotated between 1 and n times. For example, the array nums = [0,1,4,4,5,6,7] might become:
- [4,5,6,7,0,1,4] if it was rotated 4 times.
- [0,1,4,4,5,6,7] if it was rotated 7 times.
Notice that rotating an array [a[0], a[1], a[2], …, a[n-1]] 1 time results in the array [a[n-1], a[0], a[1], a[2], …, a[n-2]].
Given the sorted rotated array nums that may contain duplicates, return the minimum element of this array.
Example:
Input: nums = [2,2,2,0,1]
Output: 0
The difference between 153 and 154 is that there might be duplicate elements in the array.
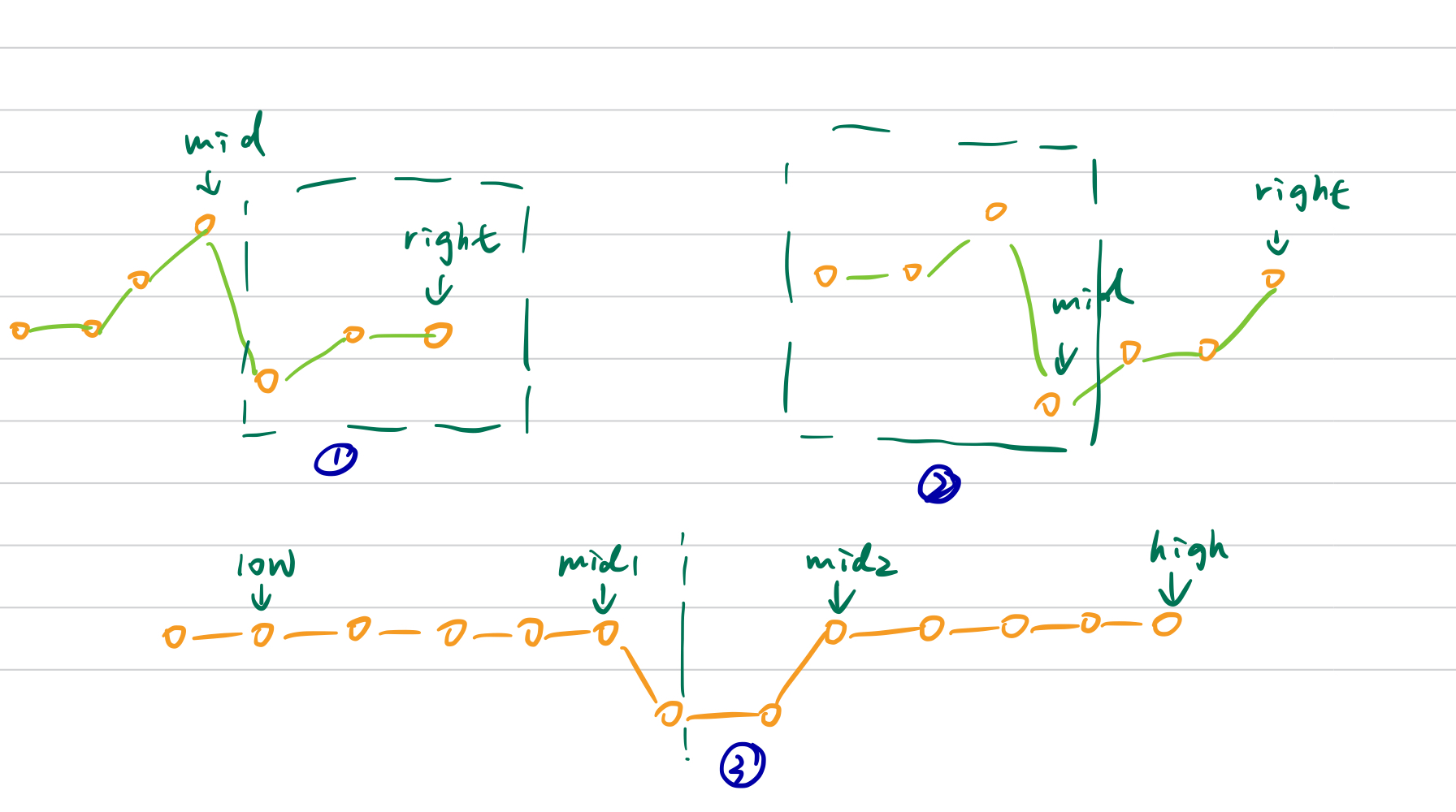
There are three cases:
- nums[mid] > nums[right]
- nums[mid] < nums[right]
The above cases are the same with 153 even if duplicates exist
- the third case: nums[mid] == nums[right]
In this case, we can move right one step left to remove the duplicates.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
def findMin(self, nums: List[int]) -> int:
left, right = 0, len(nums) - 1
while left < right:
mid = left + (right - left) // 2
if nums[right] == nums[mid]:
right -= 1
elif nums[right] > nums[mid]:
right = mid
else:
left = mid + 1
return nums[right]